前回のエッセイで「80 対20 の法則」について少し書きました｡たまたま、テレビで「カンブリア宮殿」を見ていると、パレートの法則について話をしていました。計画性の無さを露見する所業ですが、自由に書く権利を行使して、今回はちょっと寄り道です。

●パレートの法則について
有名な、80 対20 の法則・・パレートの法則の利用方法です。
経験則としてマーケットの分析に適応されています。よく見受けられるのは、
・ 売り上げ上位20%のお客様で、全体の売り上げの80%を占める。
・ 売り上げの80%は、商品の上位20%で売り上げられる。
(営業の生産性は、さらに分けて262 の法則で表されることもあります)
テレビでリサイクルショップの社長は、パレートの法則を
・ 仕入れの成約率は、80%を目標にする。
・ 仕入れたものの20%は、2 週間で売る。
・ 仕入れたものの残り80%を、2 ヶ月で売る。
など、仕入れ価格、販売価格、在庫の判断基準に利用していました。市場の実際の反応で判断する方法として、わかり易い基準にしていると感心しました。わかり易い基準の他の一例として、私の好きなブックオフさんの仕入れと販売の基準は、新しくて美本なら一律定価の10%、販売価格は、最初は定価の半額、その後105 円にする全店統一の基準だと聞いたことがあります。本の目利き、専門性を必要としないシステムを構築したことが、躍進の一因になっています。
両社とも、誰でも簡単に判断できるわかり易い基準を持っていることが共通です。

●ユダヤの法則
パレートの法則の元の考え方は、78 対22 の「ユダヤの法則」からとの説があります。
・ 22%のお金持ちが78%の資産を所有し、残りの78%の人が22%を所有する。(100 人で合計1000 万円での資産で計算すると、22 人のお金持ちは、平均１人約35.5 万円、残りは１人約2.8 万円になります。(資源を投入する対象の判断基準になります)
・ 目標の78%を達成するための、労力は22%ですむが、残りの22%を達成するためには、78%の労力を必要とする。(私は、言い訳にも使える為、特にこれは気に入っています。)

この78 対22 の法則は、図形や自然界にも見られる法則です。主なものは、
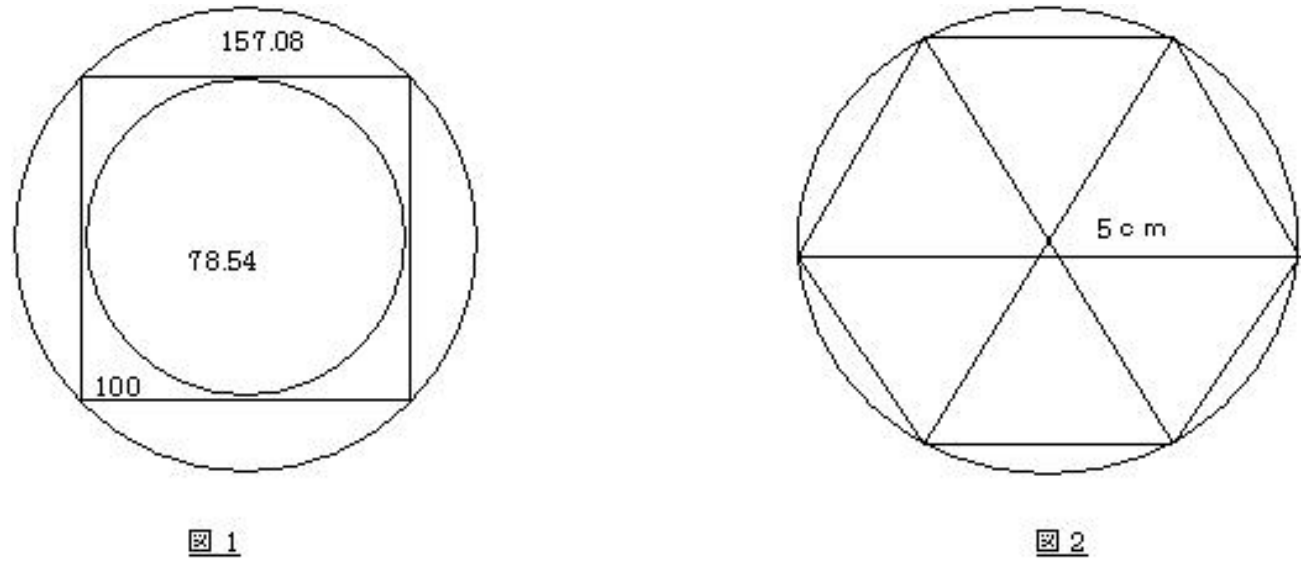
・ 四角形と中の円との面積比率の差 (100 ： 78.54) ― 図1 約22%です。
(また、四角形の外周の円の面積は、中の円の面積の倍になります)
・ 空気中の成分 (窒素 78.08%：その他 ― 酸素20.95%、アルゴン0.93% 、二酸化炭素0.034%)
二酸化酸素の排出権が時々マスコミに取り上げられています。植物は、水と光と二酸化炭素を使って、でんぷんと酸素を作り出します。日常的な出来事ですが、自然の不思議と奇跡です。酸素排出権にして、自然を守っている国に対して、何らかのメリットを付与するほうが、個人的には自然保護と、世界平和につながるのではと考えています。

●円・・・
円を1 つ描きましので、正確にかけていませんが、図２も書いてみました。円の中の六角形の周辺の長さと、円周の長さを、円の半径を5ｃｍとして計算した場合、
六角形は正三角形6 個の組み合わせですので、周辺の長さは、5ｃｍ×6＝30ｃｍ になります。
円周は、直径かける、約3.14 ですから、10ｃｍ×3.14＝31.4ｃｍ です。
二点を結ぶ最短の長さは、直線ですので、当然円周の方が長くなります。ゆとり教育が、盛んに議論されていた時期がありました。その時、円周率が難しいので、3.14 を3 にしよう。という意見があったと記憶しています。多分3 にはしなかったと思いますが、円周率を3 にした場合に、円周の長さは、10ｃｍ×3＝30ｃｍ になります。結果は、六角形の周辺の長さと同じになってしまいます。正しくないことは明らかです。正確さより、簡単さを重視する発想なのでしょうか? わかり易いことはとても大切です。しかし、それが正しいかどうか論理的に考えることは、さらに大切な習慣の一つではないでしょうか｡